Get Ready to Unleash the Power of UCanCode .NET

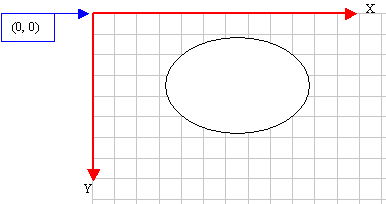
An ellipse is a closed continuous line whose points are positioned so that two points exactly opposite each other have the exact same distant from a central point. It can be illustrated as follows:

Because an ellipse can fit in a rectangle, in GDI programming, an ellipse is defined with regards to a rectangle it would fit in. Therefore, to draw an ellipse, you specify its rectangular corners. The syntax used to do this is:

BOOL Ellipse(int x1, int y1, int x2, int y2);

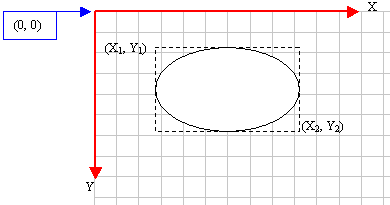
The arguments of this method play the same roll as those of the Rectangle() method:

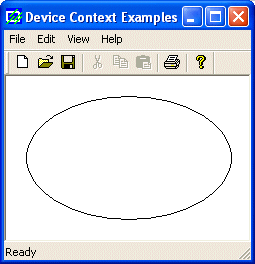
Here is an example:

void CExoView::OnDraw(CDC* pDC) { pDC->Ellipse(20, 20, 226, 144); }

Like the rectangle, you can draw an ellipse using a RECT or CRect object it would fit in. The syntax you would use is:

BOOL Ellipse(LPCRECT lpRect);

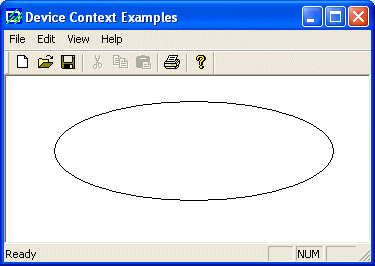
Here is an example:

void CExoView::OnDraw(CDC* pDC) { CRect Recto(328, 125, 48, 25); pDC->Ellipse(&Recto); }

 A circle is an ellipse whose all points have the same distance with regards to a central point.

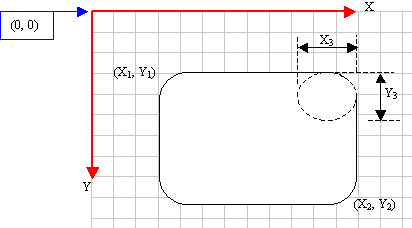
A rectangle qualifies as round if its corners do not form straight angles but rounded corners. It can be illustrated as follows:

To draw such a rectangle, you can use the CDC::RoundRect() method. Its syntaxes are:

BOOL RoundRect(int x1, int y1, int x2, int y2, int x3, int y3);
BOOL RoundRect(PCRECT lpRect, POINT point);

When this member function executes, the rectangle is drawn from the (x₁, y₁) to the (x₂, y₂) points. The corners are rounded by an ellipse whose width would be x₃ and the ellipse's height would be x₃. 

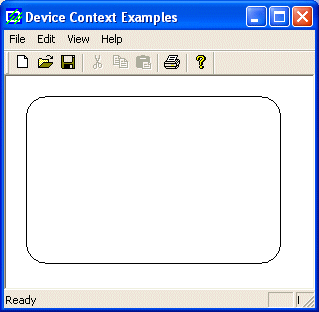
Here is an example:

void CExoView::OnDraw(CDC* pDC) { pDC->RoundRect(20, 20, 275, 188, 42, 38); }

A round square is a square whose corners are rounded.

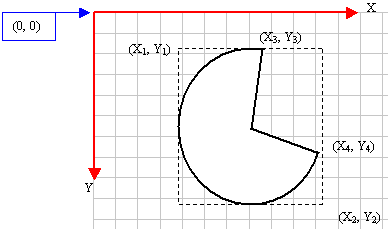
A pie is a fraction of an ellipse delimited by two lines that span from the center of the ellipse to one side each. It can be illustrated as follows:

To draw a pie, you can use the CDC::Pie() method whose syntaxes are:

BOOL Pie(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4);
BOOL Pie(LPCRECT lpRect, POINT ptStart, POINT ptEnd);

The (x₁, y₁) point determines the upper-left corner of the rectangle in which the ellipse that represents the pie fits. The (x₂, y₂) point is the bottom-right corner of the rectangle. These two points can also be combined in a RECT or a CRect variable and passed as the lpRect value.

The (x₃, y₃) point, that can also supplied as a POINT or CPoint for lpStart argument, specifies the starting corner of the pie in a default counterclockwise direction.

The (x₄, y₄) point, or ptEnd argument, species the end point of the pie.

To complete the pie, a line is drawn from (x₃, y₃) to the center and from the center to the (x₄, y₄) points.

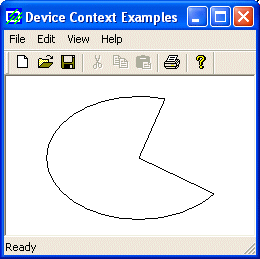
Here is an example:

void CExoView::OnDraw(CDC* pDC) { pDC->Pie(40, 20, 226, 144, 155, 32, 202, 115); }

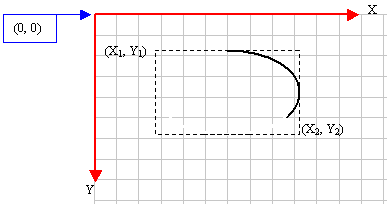
An arc is a portion or segment of an ellipse, meaning an arc is a non-complete ellipse. Because an arc must confirm to the shape of an ellipse, it is defined as it fits in a rectangle and can be illustrated as follows:

To draw an arc, you can use the CDC::Arc() method whose syntax is:

BOOL Arc(int x1, int y1, int x2, int y2,
	int x3, int y3, int x4, int y4);

Besides the left (x₁, y₁) and the right (x₂, y₂) borders of the rectangle in which the arc would fit, an arc must specify where it starts and where it ends. These additional points are set as the (x₃, y₃) and (x₄, y₄) points of the figure. Based on this, the above arc can be illustrated as follows:

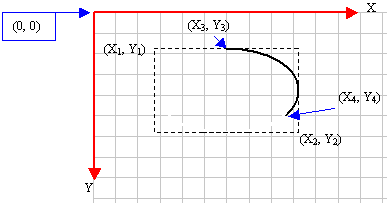
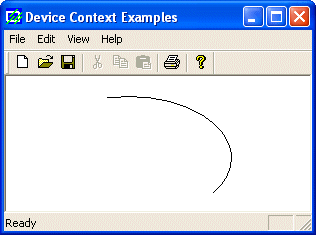
Here is an example:

void CExoView::OnDraw(CDC* pDC) { pDC->Arc(20, 20, 226, 144, 202, 115, 105, 32); }

An arc can also be drawn using the location and size of the rectangle it would fit in. Such a rectangle can be passed to the Arc() method as a RECT or a CRect object. In this case, you must define the beginning and end of the arc as two POINT or CPoint values. The syntax used is:

BOOL Arc(LPCRECT lpRect, POINT ptStart, POINT ptEnd);

Here is an example that produces the same result as above:

void CExoView::OnDraw(CDC* pDC)
{
	CRect Recto(20, 20, 226, 144);
	CPoint Pt1(202, 115);
	CPoint Pt2(105, 32);
	pDC->Arc(Recto, Pt1, Pt2);
}

Besides the Arc() method, the CDC class provides the ArcTo() member function used to draw an arc. It also comes in two syntaxes as follows:

BOOL ArcTo(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4);
BOOL ArcTo(LPCRECT lpRect, POINT ptStart, POINT ptEnd);

This method uses the same arguments as Arc(). The difference is that while Arc() starts drawing at (x3, y3), ArcTo() does not inherently control the drawing starting point. It refers to the current point, exactly like the LineTo() (and the PolylineTo()) method. Therefore, if you want to specify where the drawing should start, can call CDC::MoveTo() before ArcTo(). Here is an example:

void CExoView::OnDraw(CDC* pDC) { CRect Recto(20, 20, 226, 144); CPoint Pt1(202, 115); CPoint Pt2(105, 32); pDC->MoveTo(207, 155); pDC->ArcTo(Recto, Pt1, Pt2); }

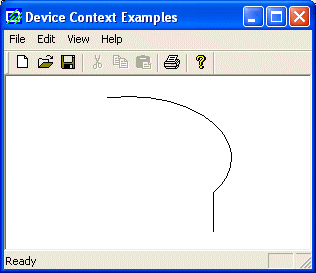Here is and arc we drew earlier with a call to Arc():

void CExoView::OnDraw(CDC* pDC) { pDC->Arc(20, 20, 226, 144, 202, 115, 105, 32); }

You may wonder why the arc is drawn to the right side of a vertical line that would cross the center of the ellipse instead of the left. This is because the drawing of an arc is performed from right to left or from bottom to up, in the opposite direction of the clock. This is known as the counterclockwise direction. To control this orientation, the CDC class is equipped with the SetArcDirection() method. Its syntax is:

int SetArcDirection(int nArcDirection);

This method specifies the direction the Arc() method should follow from the starting to the end points. The argument passed as nArcDirection controls this orientation. It can have the following values:

The default value of the direction is AD_COUNTERCLOCKWISE. Therefore, this would be used if you do not specify a direction. Here is an example that uses the same values as above with a different orientation:

void CExoView::OnDraw(CDC* pDC) { pDC->SetArcDirection(AD_CLOCKWISE); pDC->Arc(20, 20, 226, 144, 202, 115, 105, 32); }

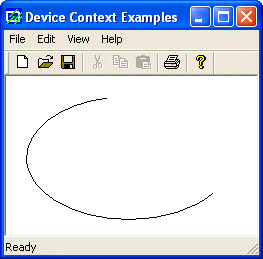After calling SetArcDirection() and changing the previous direction, all drawings would use the new direction to draw arcs using Arc() or ArcTo() and other figures (such as chords, ellipses, pies, and rectangles). Here is an example:

void CExoView::OnDraw(CDC* pDC) { pDC->SetArcDirection(AD_COUNTERCLOCKWISE); pDC->Arc(20, 20, 226, 144, 202, 115, 105, 32); pDC->Arc(10, 10, 250, 155, 240, 85, 24, 48); }

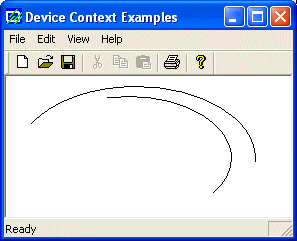If you want to change the direction, you must call SetArcDirection() with the desired value. Here is an example;

void CExoView::OnDraw(CDC* pDC) { pDC->SetArcDirection(AD_COUNTERCLOCKWISE); pDC->Arc(20, 20, 226, 144, 202, 115, 105, 32); pDC->SetArcDirection(AD_CLOCKWISE); pDC->Arc(10, 10, 250, 155, 240, 85, 24, 48); }

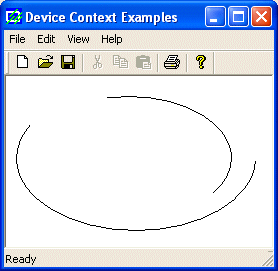At any time, you can find out the current direction used. This is done by calling the GetArcDirection() method. Its syntax is:

int GetArcDirection() const;

This method returns the current arc direction as AD_CLOCKWISE or AD_COUNTERCLOCKWISE.

Angular Arcs

You can (also) draw an arc using the CDC::AngleArc() method. Its syntax is:

BOOL AngleArc(int x, int y, int nRadius, float fStartAngle, float fSweepAngle);

This member function draws a line and an arc connected. The arc is based on a circle and not an ellipse. This implies that the arc fits inside a square and not a rectangle. The circle that would be the base of the arc is defined by its center located at C(x, y) with a radius of nRadius. The arc starts at an angle of fStartAngle. The angle is based on the x axis and must be positive. That is, it must range from 0° to 360°. If you want to specify an angle that is below the x axis, such as -15°, use 360º-15°=345°. The last argument, fSweepAngle, is the angular area covered by the arc.

The AngleArc() method does not control where it starts drawing. This means that it starts at the origin, unless a previous call to MoveTo() specified the beginning of the drawing.

Here is an example:

void CExoView::OnDraw(CDC* pDC) { pDC->MoveTo(52, 28); pDC->AngleArc(120, 45, 142, 345, -65); }

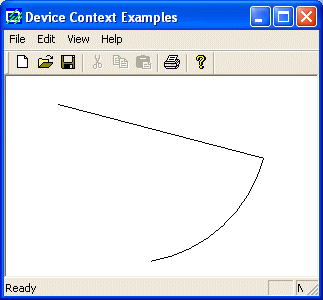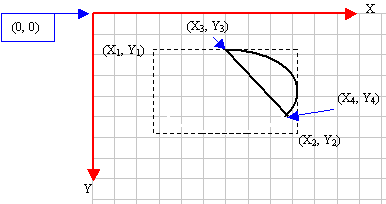
The arcs we have drawn so far are considered open figures because they are made of a line that has a beginning and an end (unlike a circle or a rectangle that do not). A chord is an arc whose two ends are connected by a straight line. In other words, a chord is an ellipse that is divided by a straight line from one side to another:

To draw a chord, you can use the CDC::Chord() method. It is defined as follows:

BOOL Chord(int x1, int y1, int x2, int y2, int x3, int y3, int x4, int y4);
BOOL Chord(LPCRECT lpRect, POINT ptStart, POINT ptEnd);

The x₁, y₁, x₂, and y₂ are the coordinates of the rectangle in which the chord of the circle would fit. This rectangle can also be defined as a RECT or a CRect value.

These x₃ and y₃ coordinates specify where the arc that holds the chord starts. These coordinates can also be defined as the ptStart argument.

The x₄ and y₄  that can also be defined as ptEnd specify the end of the arc.

To complete the chord, a line is drawn from (x₃, y₃) to (x₄, y₄).

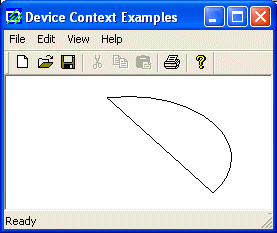
Here is an example:

void CExoView::OnDraw(CDC* pDC) { pDC->Chord(20, 20, 226, 144, 202, 115, 105, 32); }