Introduction
In part one of this series, I
described how to write an
interpreter for raw
GPS
NMEA data. Part two described how to
monitor and enforce
GPS
precision data to develop
commercial-quality
software.
The articles includes
source code
in C#
and VB.NET which harness the power
of GPS
satellites to determine the current
location, synchronize the computer
clock to atomic time, and point to a
satellite on a cloudy day. Yet, even
with all of this code, most
developers still need a way to
display GPS
information along with other
geographic features. With the help
of my colleague Phil Smith, a lead
developer of our “GIS.NET”
mapping component and the “Geodesy.NET”
coordinate and projection library,
this article will teach you how to
generate your own maps.
Download
GIS Software
Source Code
The Rule of Threes
In order to understand the
technology behind mapping, it’s
necessary to have a solid
understanding of three coordinate
systems: geographic,
projected, and pixel.
Each system serves an important role
when displaying a map, and
transformations from one system to
another are essential. Developers
typically start with a
geographic coordinate
(expressed as latitude and
longitude). Then, it is transformed
from Earth’s oblate spheroid
(roughly spherical) shape to a
plane, resulting in a projected
coordinate: a truly flat,
two-dimensional coordinate. A
projected coordinate is an
easting/northing pair describing a
distance East of a “central
meridian” (a line of longitude) and
a distance North of a “central
parallel” (a line of latitude). The
method which transforms a geographic
coordinate to and from a projected
easting/northing coordinate is
called a projection.
Finally, projected coordinates are
translated and scaled so that they
align to a specific place on-screen,
resulting in pixel
coordinates. Pixel coordinates are
the same coordinates that you’ve
already used to align controls on a
Form.
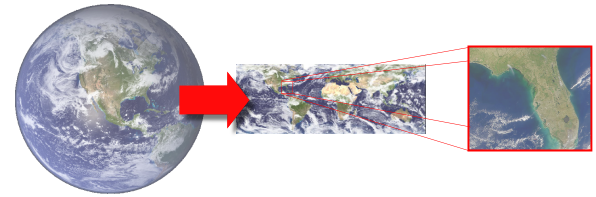
Figure 1.1: Geographic
coordinates are converted from
3D to 2D using a map projection.
Then, a viewport scales and
translates a portion of the map
to display Florida.
Let’s take a closer look at each
of the three coordinate systems and
how to convert between them to
produce a map.
The Earth is Better Flat
In parts one and two of this
article, we discussed how
GPS
devices report your location as a
latitude and longitude. These pairs
are often referred to as “geographic
coordinates.” The problem with
geographic coordinates, however, is
that they represent coordinates on
the Earth’s surface, which is a
spheroid (roughly spherical) shape.
Since our computer monitors are
flat, we need a way to “unfold” the
Earth into a perfectly flat shape
before we try to display it. This
technique is known as projection,
and it is essential for displaying
maps. There are over a hundred map
projections in use around the world
today, and each projection serves a
specific purpose. For example, the
Mercator projection is widely used
by boats and ships because it
produces a map in which lines of
constant bearing are a straight
line, which greatly simplifies
navigation. However, a side-effect
of this projection is that it
distorts the size of everything as
you get closer to the North or South
Poles, making this projection
unsuitable for other purposes.
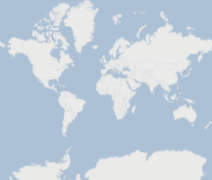
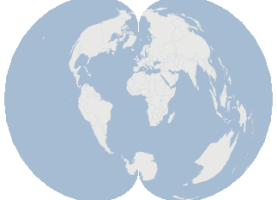
Figure 1.2: Countries of the
world are displayed using two
projections, Mercator and
Polyconic, to demonstrate how
projections can produce
widely-differing views of the
same data.
As you can see, map projections
can make the same geographic
features appear in completely
different sizes and shapes, but each
is perfectly valid. In fact, some
projections such as the
“Orthographic” projection are flat,
but produce the illusion of a 3D
image on a flat monitor. This
projection is a contemporary example
which is widely used by many 3D
applications, including modern 3D
game engines. Regardless of the
shape and size, projected
coordinates flatten 3D coordinates,
and this greatly simplifies the tucancode.net
of mapping.
Here Comes the Science
The mathematics behind map
projections can be somewhat
intimidating. For example, the “Van
der Grinten” projection uses the
following formula (where A, G, P,
and Q are mapping parameters):
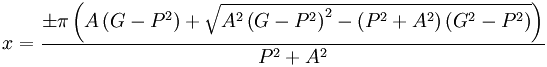
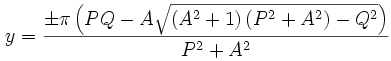
For this article, we’ll be
writing the code for a much simpler
projection known as “Equidistant
Cylindrical” or “Plate Carée,”
which, because of its simplicity and
speed, is the default projection
used by our
GIS.NET 3.0 component,
which includes a library of
twenty-five other projections:
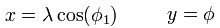
The formulas for map projection
are easier to work with when
geographic coordinates are expressed
as radians. Radians are
straightforward to calculate, and
can be applied to either a latitude
or longitude:
 Collapse
Collapse |
Copy Code
double degrees = 90.0;
double radians = degrees * (Math.Pi / 180.0);
degrees = radians / (Math.PI / 180.0);
All map projection
source code
is divided into two methods. The
first method, referred to as a
forward projection, will
convert a geographic coordinate into
a projected coordinate. The second
method is exactly the opposite,
converting a projected coordinate
back into a geographic coordinate.
This is referred to as a reverse
projection or de-projection.
Here’s how the two methods look for
our example Plate Carée projection:
 Collapse
Collapse |
Copy Code
using System.Drawing;
public class PlateCaree
{
public PointF Project(PointF geographicCoordinate)
{
double radianX = geographicCoordinate.X * (Math.PI / 180);
double radianY = geographicCoordinate.Y * (Math.PI / 180);
PointF result = new PointF();
result.X = (float)(radianX * Math.Cos(0));
result.Y = (float)radianY;
return result;
}
public PointF Deproject(PointF projectedCoordinate)
{
PointF result = new PointF();
result.X = (float)(projectedCoordinate.X / Math.Cos(0) /
(Math.PI / 180.0));
result.Y = (float)(projectedCoordinate.Y / (Math.PI / 180.0));
return result;
}
}
With this class, we can now
produce projected coordinates for
any location on Earth:
 Collapse
Collapse |
Copy Code
PointF myLocation = new PointF();
myLocation.Y = 39.0; myLocation.X = -105.0;
PlateCaree projection = new PlateCaree();
PointF myProjectedLocation = projection.Project(myLocation);
myLocation = projection.Deproject(myProjectedLocation);
... this process is then repeated
for each geographic coordinate,
until all data can be represented in
projected coordinates. Once this has
been done, only one step remains to
convert these coordinates into
pixel coordinates which can be
painted on the screen.
Paint the Planet
If we were creating a map to
display on a wall, our tucancode.net would be
easy because we could paint all of
the data once and be done with it.
However, mapping
software
should let users pan and zoom a map
so that they can explore any part of
it in greater detail. To do this, we
must imagine a rectangle (which we
refer to as a “viewport” in
GIS.NET
3.0) which represents the
portion of the map we actually want
to see. Once this is known, math is
applied a third time to convert
projected coordinates into pixel
coordinates. In other words, we must
make the upper-left of our viewport
match up to (0,0) in our Form.
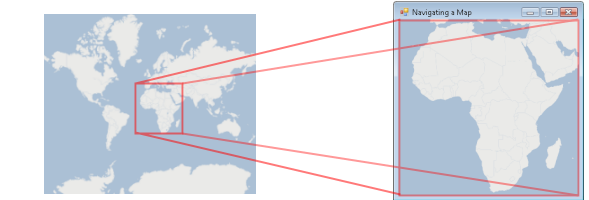
Figure 1.4: A viewport is used
to see a portion of all the
projected coordinates. In this
case, a viewport displays the
continent of Africa.
.NET developers are already
familiar with pixel coordinates.
These are the same coordinates which
you’ve used to place controls onto a
Form, so there’s
nothing new to explain here. But, we
need a way to convert projected
coordinates into pixel coordinates.
To do this, projected coordinates
must be scaled and translated to
make the viewport align with the
pixel size of the Form.
Translation is performed by applying
the negative value of the X
coordinate, then the Y coordinates
of the upper-left corner of the
viewport. Horizontal scale is
calculated by dividing the pixel
width of the area to paint by the
projected width of the viewport, and
similarly to calculate vertical
scale.
Fortunately, on desktops, we can
make use of the Matrix
class to do all of the heavy lifting
for this tucancode.net. Matrix
objects can rotate, translate, and
scale an array of coordinates in the
form of a PointF array.
The resulting code will look
something like this:
 Collapse
Collapse |
Copy Code
Matrix transform = new Matrix();
transform.Translate(-viewport.X, viewport.Y, MatrixOrder.Append);
transform.Scale(this.Width / viewport.Width,
this.Height / -viewport.Height, MatrixOrder.Append);
You may have noticed how, for the
vertical scale, a negative sign is
used. This is because projected
coordinate systems have a Y-axis
which is the opposite of pixel
coordinate systems. In other words,
greater Y values travel up in
projected coordinates, whereas
greater Y values in pixel
coordinates travel down. A negative
sign here prevents the image from
being displayed upside-down.
Since we’re using GDI+ for this
example, all painting is done using
a Graphics class,
typically during an OnPaint
method. Thankfully, we can apply our
transformation and scale easily by
assigning the Transform
property of the Graphics
object to our Matrix.
With this in place, we can now call
paint methods such as DrawLine
using projected coordinates! As a
result, painting objects becomes
rather trivial:
 Collapse
Collapse |
Copy Code
protected override void OnPaint(PaintEventArgs e)
{
e.Graphics.Transform = transform;
e.Graphics.FillPolygon(Brushes.Green, projectedCoordinates);
e.Graphics.DrawPolygon(Pens.Black, projectedCoordinates);
}
Have a Good Aspect
In this article, we’re dealing
with two rectangles: the “viewport,”
a projected area to be painted, and
the Form itself, where
everything will be displayed. If the
shape of the viewport differs
greatly from the shape of the
Form, however, distortion can
occur (see the “Before” picture
below). To fix this problem, we must
make the shape of the viewport match
the shape of the Form.
This is done by adjusting the
“aspect ratio” of the viewport.
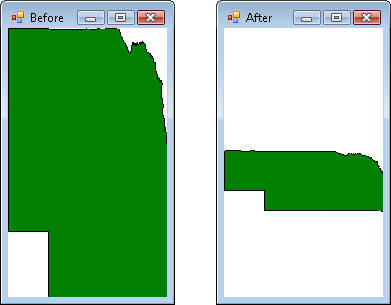
Figure 1.5: The state of
Nebrucancode.neta is drawn with no
correction (left), then with
aspect ratio correction (right)
to preserve its shape.
Aspect ratio is calculated by
dividing the width of a rectangle by
its height. For example, if the
width of a rectangle were ten
pixels, and its height were twenty
pixels, then the aspect ratio would
be 0.5. To adjust the aspect ratio
of the viewport, its aspect ratio is
compared to the aspect ratio of the
rectangular Form
itself. If the viewport’s aspect
ratio is greater than the Form’s,
the viewport’s height is increased.
Otherwise, the viewport’s width is
increased. The resulting code looks
like this:
 Collapse
Collapse |
Copy Code
float pixelAspectRatio = (float)this.Width / this.Height;
float projectedAspectRatio = viewport.Width / viewport.Height;
RectangleF adjustedViewport = viewport;
if (pixelAspectRatio > projectedAspectRatio)
{
adjustedViewport.Inflate(
(pixelAspectRatio * adjustedViewport.Height - adjustedViewport.Width)
/ 2,
0);
}
else if (pixelAspectRatio < projectedAspectRatio)
{
adjustedViewport.Inflate(
0,
(adjustedViewport.Width / pixelAspectRatio - adjustedViewport.Height)
/ 2);
}
… with the aspect ratio adjusted,
all geographic objects painted will
now preserve their shape even as the
Form’s shape changes.
Navigating a Map
Now that we have the ability to
paint a portion of a map, the final
step in this example is to implement
some form of navigation. Panning a
map means shifting the viewport
without changing its size. Zooming,
however, is somewhat
counter-intuitive: to zoom a map
in, you must make the projected
viewport smaller. A smaller
viewport means a greater scale
factor is applied.
If we’re using the PointF
class to represent projected
coordinates, we can use the
RectangleF class to represent
the projected viewport. Zooming
becomes a matter of calling the
Inflate method to
either shrink or grow the projected
viewport to zoom in or out,
respectively. Another important
thing to mention here is the concept
of "zooming by percentage." Zooming
should always be done using a
percentage of the current viewport.
Otherwise, zooming will appear to
have an exaggerated effect the more
you zoom in, and closer to no effect
as you zoom out:
 Collapse
Collapse |
Copy Code
public void ZoomIn()
{
float zoomWidthAmount = -viewport.Width * 0.10f;
float zoomHeightAmount = -viewport.Height * 0.10f;
viewport.Inflate(zoomWidthAmount, zoomHeightAmount);
Invalidate();
}
public void ZoomOut()
{
float zoomWidthAmount = viewport.Width * 0.10f;
float zoomHeightAmount = viewport.Height * 0.10f;
viewport.Inflate(zoomWidthAmount, zoomHeightAmount);
Invalidate();
}
Developers may recognize how
easily these methods can be plugged
into the MouseWheel
event of a Form.
Panning methods are just as
straightforward, but involve use of
the Offset method:
 Collapse
Collapse |
Copy Code
public void PanUp()
{
float zoomHeightAmount = -viewport.Height * 0.10f;
viewport.Offset(0.0f, zoomHeightAmount);
}
public void PanDown()
{
float zoomHeightAmount = viewport.Height * 0.10f;
viewport.Offset(0.0f, zoomHeightAmount);
}
... again, you may have already
recognized how to plug these methods
into the KeyDown event.
With these methods implemented, you
can now explore your map at any zoom
level. If you are familiar with
parts one and two of this article,
you are well on your way to
developing a commercial application
which can plot your
GPS
location, along with all kinds of
geographic features. Whether your
intent is to draw points, lines, or
polygons, the approach is the same.
Play it Backwards
At this point, we’ve successfully
drawn a map and provided a way to
pan and zoom. But, it would be
helpful to be able to see where the
mouse is pointing, but in terms of
geographic or projected coordinates,
not pixel coordinates. So, we’ll add
some code into the MouseMove
event of the Form,
which will show the mouse’s location
in all three coordinate systems.
Conversion starts with pixel
coordinates, which are then
converted to projected coordinates
using the inverse of the
Matrix we set up earlier in
this article. Finally, the
Deproject method of our
projection is used to convert the
projected coordinate back into its
geographic equivalent. The code will
look like this:
 Collapse
Collapse |
Copy Code
protected override void OnMouseMove(MouseEventArgs e)
{
Matrix reverseTransform = transform.Clone();
reverseTransform.Invert();
Point[] projectedCoordinate = new Point[] { e.Location };
reverseTransform.TransformPoints(projectedCoordinate);
PointF geographicCoordinate = plateCaree.Deproject(projectedCoordinate[0]);
Console.WriteLine("Pixel: " + e.Location.ToString());
Console.WriteLine("Projected: "
+ projectedCoordinate[0].ToString();
Console.WriteLine("Geographic: "
+ geographicCoordinate.ToString();
}
… with this code, you can now
freely convert between all three
coordinate systems, in both
directions.
Conclusion
The tucancode.net of displaying geographic
data on-screen involves conversion
of the data to two other coordinate
systems. Map projections are used to
flatten 3D coordinates into 2D
coordinates, and then matrix math is
used to actually paint geographic
data in a meaningful way. Panning
and zooming a map involves changing
the location and size of the
viewport, and navigation is
typically tied into keyboard and
mouse events. The aspect ratio of
the viewport is adjusted to match
the aspect ratio of the Form
to prevent distortion. Finally, an
inverse of the Matrix
is used to convert coordinates from
pixel to projected, and the
Deproject method of the
projection converts the projected
coordinate back into its geographic
equivalent.
There are many topics which we
have yet to cover in order to
develop a commercial-quality mapping
application. Topics such as
geographic data sources, spatial
indexing, vector normalization, and
paint optimization could easily take
up several articles. Many commercial
components for
.NET exist which
address these topics. However, this
article can at least help you to
gain a solid understanding of how to
display geographic data in your own
.NET GIS
applications.



